Riesgo relativo [RR], Razón de Momios [OR], Cociente de Riesgo [HR], Intervalo de confianza [CI], p, factores de desviación
El proposito de este artículo es proporcionar una explicación simplificada para el lector general sobre la interpretación de las investigaciones médicas.
En la literatura médica comunmente usamos tres medidas de asociación para interpretar los resultados de una investigación. Estos números son el riesgo relativo [RR], razón de momios [OR], y cociente de riesgos [HR]. La elección de cuál usar se relaciona con el diseño del estudio y el tipo de datos que se recopilaron. Afortunadamente, la mayor parte del tiempo el lector general puede interpretar las tres de una manera un poco parecida.
Riesgo relativo = RR
El riesgo relativo generalmente se utiliza en estudios prospectivos de cohortes y estudios transversales para comparar el riesgo de una persona que ha estado expuesta al riesgo de una persona que no ha estado expuesta. Generalmente se usa en estudios prospectivos de cohortes y estudios transversales.
En la literatura médica comunmente usamos tres medidas de asociación para interpretar los resultados de una investigación. Estos números son el riesgo relativo [RR], razón de momios [OR], y cociente de riesgos [HR]. La elección de cuál usar se relaciona con el diseño del estudio y el tipo de datos que se recopilaron. Afortunadamente, la mayor parte del tiempo el lector general puede interpretar las tres de una manera un poco parecida.
Riesgo relativo = RR
El riesgo relativo generalmente se utiliza en estudios prospectivos de cohortes y estudios transversales para comparar el riesgo de una persona que ha estado expuesta al riesgo de una persona que no ha estado expuesta. Generalmente se usa en estudios prospectivos de cohortes y estudios transversales.
¿Qué es un estudio prospectivo de cohortes?
Un estudio prospectivo de cohortes inscribe a un número igual de personas que están expuestas y no expuestas a un factor o tratamiento y las sigue durante un período de tiempo para ver si desarrollan el resultado de interés. Se usa para calcular la asociación entre una exposición y el resultado. La medida del efecto que se usa es el riesgo relativo.
Vemos un ejemplo de un estudio prospectivo de cohortes
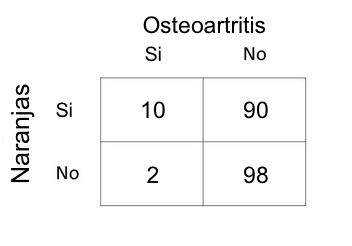
Vamos a inventar una investigación científica imaginaria. Supongamos que se hace un estudio prospectivo de cohorte comparando un caserío que se llama Villa Nueva donde hay 100 pobladores. Alli es en una zona cálida donde cultivan naranjas. Encontramos que toda la población de Villa Nueva come más de 100 naranjas al año por persona. Seguimos los 100 pobladores en Villa Nueva por 5 años y un promedio de 10 pobladores cada año desarrollan osteoartritis.
Vamos a comparar con otro caserío que se llama Palo Alto que tiene 100 pobladores. Alli es una zona montañosa de pinos donde hace frio, y nadie come naranjas. Los siguen por 5 años y encuentran un promedio de 2 pobladores cada año desarrolla síntomas de osteoartritis.
Para estudiar la correlación vamos a utilizar una tabla que nos permite calcular el Riesgo Relativo.
Un estudio prospectivo de cohortes inscribe a un número igual de personas que están expuestas y no expuestas a un factor o tratamiento y las sigue durante un período de tiempo para ver si desarrollan el resultado de interés. Se usa para calcular la asociación entre una exposición y el resultado. La medida del efecto que se usa es el riesgo relativo.
Vemos un ejemplo de un estudio prospectivo de cohortes
Vamos a inventar una investigación científica imaginaria. Supongamos que se hace un estudio prospectivo de cohorte comparando un caserío que se llama Villa Nueva donde hay 100 pobladores. Alli es en una zona cálida donde cultivan naranjas. Encontramos que toda la población de Villa Nueva come más de 100 naranjas al año por persona. Seguimos los 100 pobladores en Villa Nueva por 5 años y un promedio de 10 pobladores cada año desarrollan osteoartritis.
Vamos a comparar con otro caserío que se llama Palo Alto que tiene 100 pobladores. Alli es una zona montañosa de pinos donde hace frio, y nadie come naranjas. Los siguen por 5 años y encuentran un promedio de 2 pobladores cada año desarrolla síntomas de osteoartritis.
Para estudiar la correlación vamos a utilizar una tabla que nos permite calcular el Riesgo Relativo.
Entonces en esta tabla
a= personas expuestas al factor que desarrollan la enfermedad o el resultado que estamos estudiando
b= personas expuestas al factor que no desarrollan la enfermedad o el resultado que estamos estudiando
c= personas no expuestas al factor que desarrollan la enfermedad o el resultado que estamos estudiando
d= personas no expuestas al factor que no desarrollan la enfermedad o tienen el resultado que estamos estudiando.
a= personas expuestas al factor que desarrollan la enfermedad o el resultado que estamos estudiando
b= personas expuestas al factor que no desarrollan la enfermedad o el resultado que estamos estudiando
c= personas no expuestas al factor que desarrollan la enfermedad o el resultado que estamos estudiando
d= personas no expuestas al factor que no desarrollan la enfermedad o tienen el resultado que estamos estudiando.
Para calcular el riesgo relativo vamos a utilizar la ecuación:
Entonces en nuestro escenario
a= personas que comieron >100 naranjas con osteoartritis
b= personas que comieron > 100 naranjas sin osteoartritis
c= personas que no comieron naranjas con osteoartritis
d= personas que no comieron naranjas sin osteoartritis
a= personas que comieron >100 naranjas con osteoartritis
b= personas que comieron > 100 naranjas sin osteoartritis
c= personas que no comieron naranjas con osteoartritis
d= personas que no comieron naranjas sin osteoartritis
Ahora vamos a hacer las calculaciones que se realiza y después vamos a descubrir donde están las falacias en el estudio..
Paso 1:
Calcular el riesgo relativo =
a/a+b =(10)/10+90
c/c+d (2)/(2+98)
RR= 5
RR>1 Si el riesgo relativo es mayor que 1 quiere decir que el factor de riesgo es asociado con un aumento en la probabilidad del resultado que estamos estudiando.
RR= 1 Si el riesgo relativo hubiera resultado igual a 1 entonces el factor de riesgo no tiene ningúna correlación con la probabilidad del resultado.
RR< 1 Si el riesgo relativo es menos que 1 entonces el factor es protectivo, es decir que es asociado con menor prevalencia de la enfermedad o resultado que estamos estudiando.
Un riesgo relativo de 5,0 implica que es 5 veces más probable que esta persona desarrolla síntomas de osteoartritis durante los 5 años que los siguieron que otra persona que no comió las naranjas.
Paso 1:
Calcular el riesgo relativo =
a/a+b =(10)/10+90
c/c+d (2)/(2+98)
RR= 5
RR>1 Si el riesgo relativo es mayor que 1 quiere decir que el factor de riesgo es asociado con un aumento en la probabilidad del resultado que estamos estudiando.
RR= 1 Si el riesgo relativo hubiera resultado igual a 1 entonces el factor de riesgo no tiene ningúna correlación con la probabilidad del resultado.
RR< 1 Si el riesgo relativo es menos que 1 entonces el factor es protectivo, es decir que es asociado con menor prevalencia de la enfermedad o resultado que estamos estudiando.
Un riesgo relativo de 5,0 implica que es 5 veces más probable que esta persona desarrolla síntomas de osteoartritis durante los 5 años que los siguieron que otra persona que no comió las naranjas.
Ahora tenemos que determinar el validez de estos resultados. Para esto vamos a examinar el intervalo de confianza, el p, y buscar factores de desviación.
Paso 2 = El intervalo de confianza [CI]
El intervalo de confianza es el rango de valores donde se encuentra el verdadero valor del Riesgo Relativo. El investigador determina el tamaño de la muestra y el nivel de confianza que requiere (usualmente 95%), pero el otro factor para calcular el intervalo de confianza es la desviación estandár, que va a ser determinado por la variabilidad de los resultados. Para poder llegar a una conclusión es mejor que el rango del intervalo de confianza es estrecha y que no incluye (y si es posible no acerca) al número 1 ya que si el intervalo de confianza contiene el número uno esto implicaría que es posible que es puro casualidad y no se puede llegar a ninguna conclusión definitiva.
En el caso de nuestro ejercicio de práctica el intervalo de confianza es de 1.16 a 25., o sea que es a penitas significativo ya que es ancho, y casi casi incluye 1.
Paso 3 = determinar p
P es la probabilidad que todos los resultados pueden haber transcurrido por pura casualidad. Normalmente exigimos que p sea menos que 0,05 o sea que hay menos que 5% de probabilidad que el resultado puede haber ocurrido por casualidad.
El valor de p es directamente dependiente del número de personas que participaron en el estudio. Cuando hay un gran número de participantes en el estudio, como el número de participantes va en el denominador, esto va a bajar el p. Lo más bajo el número p, lo menos probable que puede haber ocurrido los resultados por pura casualidad. Generalmente se descalifica cualquier resultado donde p es > 0,05 es decir cualquier resultado donde hay más que un 5% de probabilidad que los resultados pueden ser por pura casualidad
En este caso otra vez hemos pasado la prueba. p =0,03
El intervalo de confianza es el rango de valores donde se encuentra el verdadero valor del Riesgo Relativo. El investigador determina el tamaño de la muestra y el nivel de confianza que requiere (usualmente 95%), pero el otro factor para calcular el intervalo de confianza es la desviación estandár, que va a ser determinado por la variabilidad de los resultados. Para poder llegar a una conclusión es mejor que el rango del intervalo de confianza es estrecha y que no incluye (y si es posible no acerca) al número 1 ya que si el intervalo de confianza contiene el número uno esto implicaría que es posible que es puro casualidad y no se puede llegar a ninguna conclusión definitiva.
En el caso de nuestro ejercicio de práctica el intervalo de confianza es de 1.16 a 25., o sea que es a penitas significativo ya que es ancho, y casi casi incluye 1.
Paso 3 = determinar p
P es la probabilidad que todos los resultados pueden haber transcurrido por pura casualidad. Normalmente exigimos que p sea menos que 0,05 o sea que hay menos que 5% de probabilidad que el resultado puede haber ocurrido por casualidad.
El valor de p es directamente dependiente del número de personas que participaron en el estudio. Cuando hay un gran número de participantes en el estudio, como el número de participantes va en el denominador, esto va a bajar el p. Lo más bajo el número p, lo menos probable que puede haber ocurrido los resultados por pura casualidad. Generalmente se descalifica cualquier resultado donde p es > 0,05 es decir cualquier resultado donde hay más que un 5% de probabilidad que los resultados pueden ser por pura casualidad
En este caso otra vez hemos pasado la prueba. p =0,03
Entonces
RR = 5, 0
CI [1.16 -25]
p<0,03
Hemos satisfecho todas las condiciones, pero no hemos visto si hay factores de desviación. ¿Puedo concluir que comer naranjas aumenta la probabilidad de desarrollar osteoartritis? No, no se puede. Aunque el RR es impresionante, el CI es pasable, y el p es bueno, hay un factor más. Un factor de desviación.
Variables de confusión Confounding factors
Un variable de confusión es un dato que no es la verdadera explicación del fenómeno sino que es relacionado con la exposición y el resultado.
En nuestro ejemplo hay un tercer variable que está provocando confusión.
Lo que nos faltó averiguar es que en Villa Nueva 65% de la población es mayor de 65 años, es decir que la gente de la tercera edad han mudado alli por que la clima es más agradable. Esta clima cálida hace posible cultivar y comer naranjas mientras que en Palo Alto solo 2% de la población son mayores de 65 años. O sea que el factor de desviación era la edad de la población ya que personas mayores desarrollan más osteoartritis
.
No se puede atribuir el mayor número de personas con osteoartritis al consumo de naranjas porque las dos poblaciones no son comparables. La edad promedia de la población de Villa Nueva es mucho mayor que la población de Palo Alto.
Conclusión: En el diseño de un estudio prospectivo de cohortes es importante asegurarse que las poblaciones son comparables.
Ahora en una investigación científica moderna siempre van a tomar en cuenta la edad. Pero igual podría haber otro factor que produce confusion. Por ejemplo podría ser que en Villa Nueva hay maras, o que no hay médicos, o que es un pueblo más pobre. Asi que cautela con la interpretación de los RR, hay que buscar los variables confusos. En general se puede suponer que si es un buen estudio ya tomaron las medidas necesarias para asegurar que han comparado poblaciones comparables, es decir de la misma edad etc.
¿Qué es un estudio transversal?
Un estudio transversal demuestra la prevalencia de una enfermedad, y la exposición de toda una población en un solo momento. Tiene varios limitantes. Aquí se incluye que no se puede determinar si la exposición ocurrió antes del resultado, e incluso si las mismas personas que tienen la exposición tienen la enfermedad. El estudio transversal es particularmente sujeto a variables confusas, es decir factores que causan confusión. El estudio transversal funciona principalmente para demostrar la prevalencia de una enfermedad y de factores de riesgo pero no se puede llegar a conclusiones sobre la causación.
¿Qué es un razón de momios/ odds ratio [OR]?
Odds ratio [OR] mide la asociación entre una exposición y un resultado en una investigación retrospectiva. Odds ratio se usa en los estudios de casos y controles para comparar las probabilidades de que un evento ocurrió en un grupo expuesto en comparación con las probabilidades de que un evento ocurrión en un grupo no expuesto. En otras palabras, es para determinar las probabilidades de que un evento ocurra en personas expuestas a un factor de riesgo particular por las probabilidades de que un evento no ocurra. La odds ratio es similar al riesgo relativo de enfermedades poco comunes, pero puede exagerar los resultados cuando se trata de enfermedades comunes. Es por esta razón que generalmente es más riguroso usar el riesgo relativo, y por lo tanto las investigaciones prospectivas de cohorte. Probabilidades de un evento en el grupo de tratamiento / Probabilidades de un evento en el grupo de control
= ad / bc
Aquí vemos un fragmento de un estudio reciente verdadero publicado en BMJ que utilizó razón de momios. "Se adquirió una cohorte de 446 763 individuos, incluyendo 61 460 con infarto agudo de miocardio. Tomar cualquier dosis de AINES durante una semana, un mes o más de un mes se asoció con un mayor riesgo de infarto de miocardio..las odds ratios [OR] correspondientes (95% intervalo de confianza) fueron 1.24 (0.91 a 1.82) para celecoxib, 1.48 (1.00 a 2.26) para ibuprofeno, 1.50 (1.06 a 2.04) para diclofenaco, 1.53 (1.07 a 2.33) para naproxeno y 1.58 ( 1.07 a 2.17) para rofecoxib."
Bally M, Dendukuri N, Rich B. Risk of acute myocardial infarction with NSAIDS in real world use: bayesian meta-analysis of real world data. BMJ 2017; 357:j1909
¿Qué podemos concluir sobre los resultados?
A pesar que que se nota un aumento en el odds ratio de infarto de miocardio asociado con celecoxib e ibuprofeno, el intervalo de confianza incluye 1, y el intervalo de confianza es bastante ancho. En este caso la desviación estandar es ancho y todavía existe una posibilidad que el aumento de probabilidad sea casualidad entre el grupo que utilizó celecoxib e ibuprofeno. No es así en el caso de diclofenaco, naproxeno o rofecoxib, porque el intervalo de confianza no incluye 1. Se puede concluir que el aumento de riesgo de infarto de miocardio con el uso de diclofenaco, naproxeno y rofecoxib es significativo.
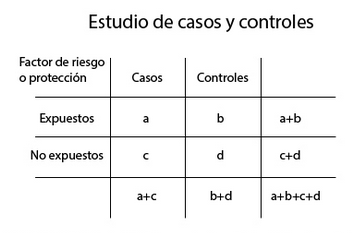
Estudios retrospectivos de casos y controles
Un estudio de control de casos comienza con la enfermedad y retrocede en el tiempo en busca de exposiciones. La medida de asociación que se usa se llama odds ratio.
Esto calculará las probabilidades de estar expuesto si tiene el resultado dividido por las probabilidades de estar expuesto si no tiene el resultado.
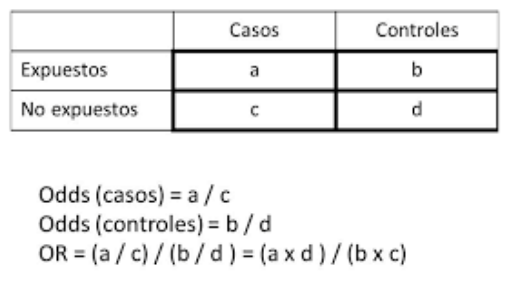
Aquí mostraremos nuestra tabla de contingencia 2x2
Lo que nos faltó averiguar es que en Villa Nueva 65% de la población es mayor de 65 años, es decir que la gente de la tercera edad han mudado alli por que la clima es más agradable. Esta clima cálida hace posible cultivar y comer naranjas mientras que en Palo Alto solo 2% de la población son mayores de 65 años. O sea que el factor de desviación era la edad de la población ya que personas mayores desarrollan más osteoartritis
.
No se puede atribuir el mayor número de personas con osteoartritis al consumo de naranjas porque las dos poblaciones no son comparables. La edad promedia de la población de Villa Nueva es mucho mayor que la población de Palo Alto.
Conclusión: En el diseño de un estudio prospectivo de cohortes es importante asegurarse que las poblaciones son comparables.
Ahora en una investigación científica moderna siempre van a tomar en cuenta la edad. Pero igual podría haber otro factor que produce confusion. Por ejemplo podría ser que en Villa Nueva hay maras, o que no hay médicos, o que es un pueblo más pobre. Asi que cautela con la interpretación de los RR, hay que buscar los variables confusos. En general se puede suponer que si es un buen estudio ya tomaron las medidas necesarias para asegurar que han comparado poblaciones comparables, es decir de la misma edad etc.
¿Qué es un estudio transversal?
Un estudio transversal demuestra la prevalencia de una enfermedad, y la exposición de toda una población en un solo momento. Tiene varios limitantes. Aquí se incluye que no se puede determinar si la exposición ocurrió antes del resultado, e incluso si las mismas personas que tienen la exposición tienen la enfermedad. El estudio transversal es particularmente sujeto a variables confusas, es decir factores que causan confusión. El estudio transversal funciona principalmente para demostrar la prevalencia de una enfermedad y de factores de riesgo pero no se puede llegar a conclusiones sobre la causación.
¿Qué es un razón de momios/ odds ratio [OR]?
Odds ratio [OR] mide la asociación entre una exposición y un resultado en una investigación retrospectiva. Odds ratio se usa en los estudios de casos y controles para comparar las probabilidades de que un evento ocurrió en un grupo expuesto en comparación con las probabilidades de que un evento ocurrión en un grupo no expuesto. En otras palabras, es para determinar las probabilidades de que un evento ocurra en personas expuestas a un factor de riesgo particular por las probabilidades de que un evento no ocurra. La odds ratio es similar al riesgo relativo de enfermedades poco comunes, pero puede exagerar los resultados cuando se trata de enfermedades comunes. Es por esta razón que generalmente es más riguroso usar el riesgo relativo, y por lo tanto las investigaciones prospectivas de cohorte. Probabilidades de un evento en el grupo de tratamiento / Probabilidades de un evento en el grupo de control
= ad / bc
Aquí vemos un fragmento de un estudio reciente verdadero publicado en BMJ que utilizó razón de momios. "Se adquirió una cohorte de 446 763 individuos, incluyendo 61 460 con infarto agudo de miocardio. Tomar cualquier dosis de AINES durante una semana, un mes o más de un mes se asoció con un mayor riesgo de infarto de miocardio..las odds ratios [OR] correspondientes (95% intervalo de confianza) fueron 1.24 (0.91 a 1.82) para celecoxib, 1.48 (1.00 a 2.26) para ibuprofeno, 1.50 (1.06 a 2.04) para diclofenaco, 1.53 (1.07 a 2.33) para naproxeno y 1.58 ( 1.07 a 2.17) para rofecoxib."
Bally M, Dendukuri N, Rich B. Risk of acute myocardial infarction with NSAIDS in real world use: bayesian meta-analysis of real world data. BMJ 2017; 357:j1909
¿Qué podemos concluir sobre los resultados?
A pesar que que se nota un aumento en el odds ratio de infarto de miocardio asociado con celecoxib e ibuprofeno, el intervalo de confianza incluye 1, y el intervalo de confianza es bastante ancho. En este caso la desviación estandar es ancho y todavía existe una posibilidad que el aumento de probabilidad sea casualidad entre el grupo que utilizó celecoxib e ibuprofeno. No es así en el caso de diclofenaco, naproxeno o rofecoxib, porque el intervalo de confianza no incluye 1. Se puede concluir que el aumento de riesgo de infarto de miocardio con el uso de diclofenaco, naproxeno y rofecoxib es significativo.
Estudios retrospectivos de casos y controles
Un estudio de control de casos comienza con la enfermedad y retrocede en el tiempo en busca de exposiciones. La medida de asociación que se usa se llama odds ratio.
Esto calculará las probabilidades de estar expuesto si tiene el resultado dividido por las probabilidades de estar expuesto si no tiene el resultado.
Aquí mostraremos nuestra tabla de contingencia 2x2
a = número de personas expuestas y con enfermedad
b = número de personas expuestas pero sin enfermedad
c = número de personas no expuestas pero con enfermedad
d = número de personas no expuestas: y sin enfermedad
En resumen lo minimo que se debe hacer para interpretar el odds ratio es:
1- Ver cual es el odds ratio para determinar cuanto es la probabilidad.
2- Ver el intervalo de confianza para determinar la consistencia interna de los datos. El intervalo de confianza es más confiable si es estrecho y no incluye el número 1. Si es muy cerca de 1 entonces es posible que la asociación no es fuerte, si es muy ancho el rango quiere decir que había mucha variabilidad en los datos.
3- Analizar el p para ver si p <0,05. Recuerda que un mayor número de participantes va a bajarr el p. Por esto se realiza estudios multicentricos con cientos de miles de participantes, para aumentar el tamaño de la muestra y bajar el p. Cuando el p es bajo se dice que el estudio tiene mucho poder.
4- Buscar factores de desviación que pueden haber sido el verdadero factor determinante.
b = número de personas expuestas pero sin enfermedad
c = número de personas no expuestas pero con enfermedad
d = número de personas no expuestas: y sin enfermedad
En resumen lo minimo que se debe hacer para interpretar el odds ratio es:
1- Ver cual es el odds ratio para determinar cuanto es la probabilidad.
2- Ver el intervalo de confianza para determinar la consistencia interna de los datos. El intervalo de confianza es más confiable si es estrecho y no incluye el número 1. Si es muy cerca de 1 entonces es posible que la asociación no es fuerte, si es muy ancho el rango quiere decir que había mucha variabilidad en los datos.
3- Analizar el p para ver si p <0,05. Recuerda que un mayor número de participantes va a bajarr el p. Por esto se realiza estudios multicentricos con cientos de miles de participantes, para aumentar el tamaño de la muestra y bajar el p. Cuando el p es bajo se dice que el estudio tiene mucho poder.
4- Buscar factores de desviación que pueden haber sido el verdadero factor determinante.
¿Qué es un cociente de riesgo/ hazard ratio [HR]?
Esta es la posibilidad de que en un momento dado ocurra un evento dado que aún no ha sucedido. Se usa en el análisis de supervivencia. Compara la probabilidad relativa de que una persona tenga un evento (como infarto de miocardio, accidente cerebrovascular, diagnóstico de cáncer) en un período de tiempo determinado. El cálculo de la relación de riesgo es complejo y va más allá del alcance de este artículo.
HR <1 El grupo de tratamiento tiene menos riesgo que el no expuesto. La exposición es protectora.
HR = 1 No hay diferencia entre los dos grupos
HR> 1 El grupo de tratamiento tiene más riesgo que el no expuesto. La exposición es dañino
Aquí vamos a interpretar un artículo reciente publicado en JAMA.
Un total de 1.44 millones de participantes (mediana [rango] de edad, 59 [19-98] años, 57% mujeres) con 186 932 cánceres fueron incluidos en la investigación. Niveles altos o bajos de actividad física durante el tiempo libre se asociaron con menor riesgo de 13 cánceres: adenocarcinoma esofágico (HR, 0.58; 95% IC, 0,37-0,89), hígado (HR, 0,73, IC del 95%, 0,55-0,98), pulmón (HR, 0,74; IC del 95%, 0,71-0,77), riñón (HR, 0,77; IC del 95%, 0,70-0,85), cardias (HR, 0,78, IC del 95%, 0,64-0,95), endometrio (HR, 0,79; IC 95%, 0.68-0.92), leucemia mieloide (HR, 0.80, IC 95%, 0.70-0.92), mieloma (HR, 0.83; IC del 95%, 0,72-0,95), colon (CRI, 0,84; IC del 95%, 0,77-0,91), cabeza y cuello (CRI, 0,85; 95% IC, 0,78-0,93), rectal (HR, 0,87; IC del 95%, 0,80-0,95), vejiga (HR, 0,87; IC del 95%, 0,82-0,92), y mama (HR, 0,90; IC del 95%, 0,87-0,93).
Moore SC, Lee I, Weiderpass E, et al. Association of Leisure-Time Physical Activity With Risk of 26 Types of Cancer in 1.44 Million Adults. JAMA Intern Med. 2016;176(6):816–825.
Si se analiza estos datos se encuentra que el ejercicio disminuye el riesgo para todos los 13, y en todos los casos el intervalo de confianza no incluye 1 por lo que se puede decir que es improbable que este se debe a pura casualidad. El cáncer que mejor responde al ejercicio es la adenocarcinoma esofágico y el que menos responde es el cáncer de mama.
Esta es la posibilidad de que en un momento dado ocurra un evento dado que aún no ha sucedido. Se usa en el análisis de supervivencia. Compara la probabilidad relativa de que una persona tenga un evento (como infarto de miocardio, accidente cerebrovascular, diagnóstico de cáncer) en un período de tiempo determinado. El cálculo de la relación de riesgo es complejo y va más allá del alcance de este artículo.
HR <1 El grupo de tratamiento tiene menos riesgo que el no expuesto. La exposición es protectora.
HR = 1 No hay diferencia entre los dos grupos
HR> 1 El grupo de tratamiento tiene más riesgo que el no expuesto. La exposición es dañino
Aquí vamos a interpretar un artículo reciente publicado en JAMA.
Un total de 1.44 millones de participantes (mediana [rango] de edad, 59 [19-98] años, 57% mujeres) con 186 932 cánceres fueron incluidos en la investigación. Niveles altos o bajos de actividad física durante el tiempo libre se asociaron con menor riesgo de 13 cánceres: adenocarcinoma esofágico (HR, 0.58; 95% IC, 0,37-0,89), hígado (HR, 0,73, IC del 95%, 0,55-0,98), pulmón (HR, 0,74; IC del 95%, 0,71-0,77), riñón (HR, 0,77; IC del 95%, 0,70-0,85), cardias (HR, 0,78, IC del 95%, 0,64-0,95), endometrio (HR, 0,79; IC 95%, 0.68-0.92), leucemia mieloide (HR, 0.80, IC 95%, 0.70-0.92), mieloma (HR, 0.83; IC del 95%, 0,72-0,95), colon (CRI, 0,84; IC del 95%, 0,77-0,91), cabeza y cuello (CRI, 0,85; 95% IC, 0,78-0,93), rectal (HR, 0,87; IC del 95%, 0,80-0,95), vejiga (HR, 0,87; IC del 95%, 0,82-0,92), y mama (HR, 0,90; IC del 95%, 0,87-0,93).
Moore SC, Lee I, Weiderpass E, et al. Association of Leisure-Time Physical Activity With Risk of 26 Types of Cancer in 1.44 Million Adults. JAMA Intern Med. 2016;176(6):816–825.
Si se analiza estos datos se encuentra que el ejercicio disminuye el riesgo para todos los 13, y en todos los casos el intervalo de confianza no incluye 1 por lo que se puede decir que es improbable que este se debe a pura casualidad. El cáncer que mejor responde al ejercicio es la adenocarcinoma esofágico y el que menos responde es el cáncer de mama.


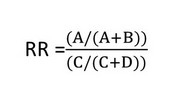
 RSS Feed
RSS Feed